NumPy est l’une des bibliothèques python les plus populaires. L’objectif de cet article sera de présenter les fonctionnalités principales proposées par NumPy et bien plus !
NumPy (Numerical Python) est la bibliothèque la plus populaire de calcul scientifique en Python. Ainsi, elle permet d’effectuer les calculs scientifiques de base et de manipuler assez facilement les tableaux multidimensionnels. En gros NumPy permet de faire :
- de l’Analyse numérique
- de l’Algèbre Linéaire
- du Calcul matriciel
- …
Comment installer NumPy ?
Si vous avez déjà installé la distribution Anaconda (sinon cliquez ici savoir comment l’installer rapidement) il vous suffit d’installer NumPy comme suit :
conda install numpy
ou via l’installateur de paquet python pip comme suit :
pip install numpy
L’import de la bibliothèque NumPy se fait comme suit :
import numpy as np
rien de nouveau 😉
Avant d’aller plus loin essayons de comprendre la notion de tableaux multidimensionnels.
Comprendre les tableaux multidimensionnels
Par définition un tableau ou Array en anglais est une structure de données constituée d’une collection d’élément (du même type) identifié par un index .

Les éléments de ce tableau sont stockés dans des emplacements de mémoire contigus. L’idée est de stocker plusieurs éléments du même type ensemble dans le but d’améliorer les performances de calcul.
❗️Attention, Il ne faut pas confondre les listes et les tableaux qui sont deux structures de données semblables.La grande différence entre ces deux structures de données se trouve au niveau des fonctions que vous pouvez leur appliquer. Par exemple, vous pouvez diviser un tableau (valeurs numériques) par 5, et chaque nombre dans le tableau sera divisé par 5 et vous aurez le résultat voulu. Cependant, si vous essayez de diviser une liste (valeurs numériques) par 5, l’interpréteur Python vous retournera une erreur.
L’image précédente est un exemple d’un tableau à une dimension. Ainsi, on parlera de tableaux multidimensionnels lorsqu’on aura au minimum deux dimensions 🙃.
On peut définir la dimension d’un tableau comme le nombre d’indices (d’axes) nécessaires pour spécifier de manière unique un élément dans le tableau. Essayons d’analyser l’exemple suivant. Dans cet exemple il s’agit d’un ensemble de données représentant les notes sur 20 de 4 élèves. Il est évidement qu’il s’agit d’un tableau à deux dimensions dont les axes sont les élèves et les notes.
| Note 1 | Note 2 | Note 3 | |
|---|---|---|---|
| Evan | 12 | 11 | 13 |
| Bernard | 14 | 14 | 8 |
| Jules | 08 | 06 | 10 |
| Eddy | 18 | 17 | 18 |
L’intérêt des dimensions ou axes est qu’ils nous permettent d’analyser et traiter des données sous plusieurs angles. Dans notre cas on peut par exemple avoir la moyenne par étudiant ou par évaluation.
Nous sommes dans un cas assez simple en deux dimensions mais on a aussi des exemples assez classiques en 3 dimensions et plus : Une image est par exemple en 3 dimensions (la hauteur, la largeur et le nombre de canaux)

L’image ci-dessus nous présente des exemples de tableaux de une, deux et trois dimensions. (C’est un peu plus compliqué de représenter les dimensions supérieures à 3).
Bon on referme cette grande parenthèse et on reprends avec NumPy.
Les Bases
1. créer un tableau NumPy
Pour créer un tableau (d’une dimension) NumPy il suffit d’utiliser la fonction « array() » comme suit :
a = np.array([1,2,3])
après bien évidement avoir importé la bibliothèque comme présenté plus haut.
Pour créer un tableau à deux dimensions ou une matrice (4×3 dans notre exemple), il suffit d’assigner une liste de tuple ou chaque tuple correspond à une ligne de notre matrice.
b = np.array([(1,2,3), (4,5,6) , (7,8,9), (10,11,12)])
On peut même utiliser des tableaux en lieu et place des tuples
b = np.array([ [1,2,3], [4,5,6] , [7,8,9], [10,11,12]])
Pour des tableaux en 3 dimensions (3x3x3 dans notre exemple)on procède comme suit
c = np.array([[[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8]], [[ 9, 10, 11], [12, 13, 14], [15, 16, 17]], [[18, 19, 20], [21, 22, 23], [24, 25, 26]]])
Je crois que vous avez compris le principe : en dimension 1 on a une liste, en dimension 2 on a une liste de liste, en dimension 3 on liste de liste de liste, … , en dimension N on a une liste de N – 1 listes imbriquées 😎.
On peut aussi créer un tableau de zeros avec la fonction « zeros »
# Un tableau en 2-D de zéros de 2 lignes et 3 colones d = np.zeros((2,3))
ou même un tableau de « 1 » avec la fonction « ones ».
# Un tableau en 2-D de uns de 2 lignes et 3 colones d = np.ones((2,3))
De plus, il est possible de générer un tableau 1-D d’une suite de nombre. Par exemple un tableau qui contient les nombre de 10 à 20 ou tous les nombre paires entre 0 et 20. Cela se fait grace à la fonction « arange() »
# Un tableau de nombres compris entre 10 et 20 e = np.arange(10,21) # Un tableau des nombres paires compris entre 0 et 20 f = np.arange(0,20,2)
On peut aussi créer la matrice identité avec NumPy.
Cette matrice correspond à un tableau en 2D avec des uns sur la diagonale et des zéros ailleurs.
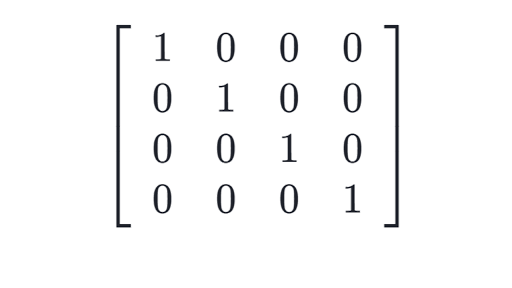
# Matrice identité 3x3 g = np.eyes(3)
Il est aussi possible de générer des nombres aléatoires compris entre 0 et 1 avec la fonction « random.random() »
# un nombre aléatoire alea = np.random.random() # un tableau de N nombres aléatoires N=3 h = np.random.random(N)
2. Les différents types de données
Dans la section précédente nous nous sommes attelés à créer des tableaux NumPy sans se soucier du type des données à l’intérieur de ces tableaux. Cependant, il faut savoir c’est que toutes valeurs d’un tableau NumPy on le même type, il est donc fortement recommandé de spécifier le type des données lors de la création d’un array NumPy. Un exemple de quelques types ci-dessous :
np.float32
np.int64
np.complex
np.bool
np.string_
Voyons comment spécifier le type d’un tableau NumPy.
#un tableau d'entier a = np.array([1,2,3], dtype=np.int16) #un tableau de float a_float = np.array([1,2,3], dtype=float) #un tableau de complex a_complex = np.array([1,2,3], dtype=np.complex)
3. Importer ou exporter des données
Si vous voulez enregistrer un tableau dans un fichier (binaire) vous il suffit d’utiliser la fonction « save()« , pour plusieurs tableaux il existe la fonction « savez ». Par contre, si vous voulez enregistrer vos tableaux dans des fichiers textes il existe aussi la fonction « savetxt() »
#Enregistrer un tableau dans un fichier binaire
np.save('my_array', a)
#Enregistrer plusieurs tableaux
np.savez('many_array.npz', a, b,c)
#Enregistrer un tabeau dans un fichier texte
np.savetxt('myTextArray.txt';, a, delimiter=' ; ')
Dans l’autre sens pour charger ces fichiers qu’on vient de créer, on passe par les fonctions « load() » et « loadtxt() » (pour les fichiers textes).
4. Quelques informations sur vos tableaux NumPy
Quand on manipule des tableaux NumPy, on aime souvent avoir quelques informations assez basiques sur notre tableau (les dimensions du tableau, le nombre d’éléments dans le tableau, le type, …).
# La forme du tableau ex (3x3) ou (4x2x2) a.shape # Nombre d'éléments dans le tableau. len(a) # Nombre de dimensions du tableau. b.ndim # Le nombre total de valeurs contenues dans le tableau. d.size #Le type du tableau b.dtype
Les Calculs et les Opérations
1. Opérations mathématiques
L’une des forces de NumPy est de proposer fonctions natives mieux adaptées aux opérations arithmétiques sur les tableaux. Il est possible d’effectuer l’addition avec add(), la soustraction subtract(), la multiplication avec multiply() et division avec divide(). Il est même possible de faire un produit scalaire avec la fonction dot() !
# Opérations arithmétiques de base np.subtract(a,b) np.add(b,a) np.multiply(a,b) # produit scalaire de deux vecteurs f = np.arange(1,11) g = np. arange(1,21,2) f.dot(g)
De plus, que serait une bibliothèque de calcul sans les fonctions classiques (fonction exponentielle, cosinus, sinus,…)! Alors NumPy ne déroge pas à la règle toutes les fonctions mathématiques sont bien présentes ! Quelques exemples ci-dessous :
np.exp(b) np.sqrt(b) np.sin(a) np.cos(b) np.log(a)
2. Les Comparaisons
Bon imaginons que nous avons deux tableaux dont nous voulons comparer uniquement les valeurs sans faire d’itération, NumPy nous permet de le faire assez aisément. Suivons cet exemple
#On a deux tableaux f et g créés précédemment. On aimerait savoir si f = E(g/2 + tetha) + 1 # où E est la fonction partie entière et thetha une valeur très petite proche de 0 ( inférieur à 1) #on fixe thetha a 0.00001 thetha = 0.00001 #On fait la comparaison avec == (floor() représente la fonction partie entière) f == np.floor(g/2 + thetha) + 1 """ Le résultat array([ True, True, True, True, True, True, True, True, True,True]) """
3. Les Agrégations
Avec NumPy, il est possible de faire plein de choses assez intéressantes en une ligne comme faire la somme des éléments dans un tableau, avoir la plus grande valeur du tableau… je vous laisse voir vous même avec l’exemple ci-dessous
#Somme des éléments du tableau sur un axe donné. a.sum() #le minimum, maximum le long d'un axe donné. a.min() b.max(axis=0) #La moyenne arithmétique, la médiane le long d'un axe donné a.mean() b.median() #matrice de corrélation np.corrcoef(b) #L'écart type le long d'un axe donné np.std(b)
La manipulation des tableaux NumPy
L’accès aux valeurs contenues dans un tableau NumPy se fait de la même manière que les listes python. Aussi, ce qui est intéressant avec cette bibliothèque e’st qu’on peut sélectionner des éléments du tableau en fonction de certaines conditions (les éléments de la liste inférieurs à 3 par exemple)
#les éléments inférieurs à 3 f[f < 3]
De plus on peut effecteur des opérations de transposée avec « transpose()« , modifier la forme d’un tableau avec « reshape » ou même fusionner deux tableaux avec « concatenate()« .
#Transposition d'un tableau b_transpose = np.transpose(b) #Reshape: Donne une nouvelle forme à un tableau sans modifier ses données. #f en shape (10,) en shape (5,2) f_reshape = f.reshape(5,2) #concatenation de deux tableaux np.concatenate((f,g), axis=0)
Conclusion
Dans cet article nous avons essayé de disséquer pas à pas la célèbre bibliothèque Python de calcul numérique NumPy. Cette bibliothèque permet d’effectuer un grand nombre d’opérations et est vraiment nécessaire pour l’analyse de données avec Python.
N’oubliez pas de vous abonner et de laisser un petit commentaire 😉 .



