Dans cet article nous allons présenter un des concepts de base de l’analyse de données : la régression linéaire. Nous commencerons par définir théoriquement la régression linéaire puis nous allons implémenter une régression linéaire sur le “Boston Housing dataset“ en python avec la librairie scikit-learn .
C’est quoi la régression linéaire ?
Une régression a pour objectif d’expliquer une variable Y par une autre variable X. Par exemple on peut expliquer les performances d’un athlète par la durée de son entrainement ou même le salaire d’une personne par le nombre d’années passées à l’université. Dans notre cas on s’intéresse à la régression linéaire qui modélise la relation entre X et Y par une équation linéaire.

β0 et β1 sont les paramètres du modèle
ε l’erreur d’estimation
Y variable expliquée
X variable explicative.
Dans ce cas on parle de régression linéaire simple car il y a une seule variable explicative. Ainsi on parlera de régression linéaire multiple lorsqu’on aura au moins deux variables explicatives.
Pour approfondir vos connaissances à ce sujet vous pouvez cliquer ici .
Passons à l’étape suivante :
Création d’un modèle de régression linéaire
Dans cette partie le jeu de données que nous allons utiliser est le suivant :
Boston Housing Dataset , sa description est disponible ici : Boston Housing data
En gros ce jeu de données comprend le prix des maisons dans les différentes zones de Boston.
L’objectif sera de prédire le prix des maisons (variable expliquée) grâce aux différentes informations présentes dans le jeu de données (variables explicatives).
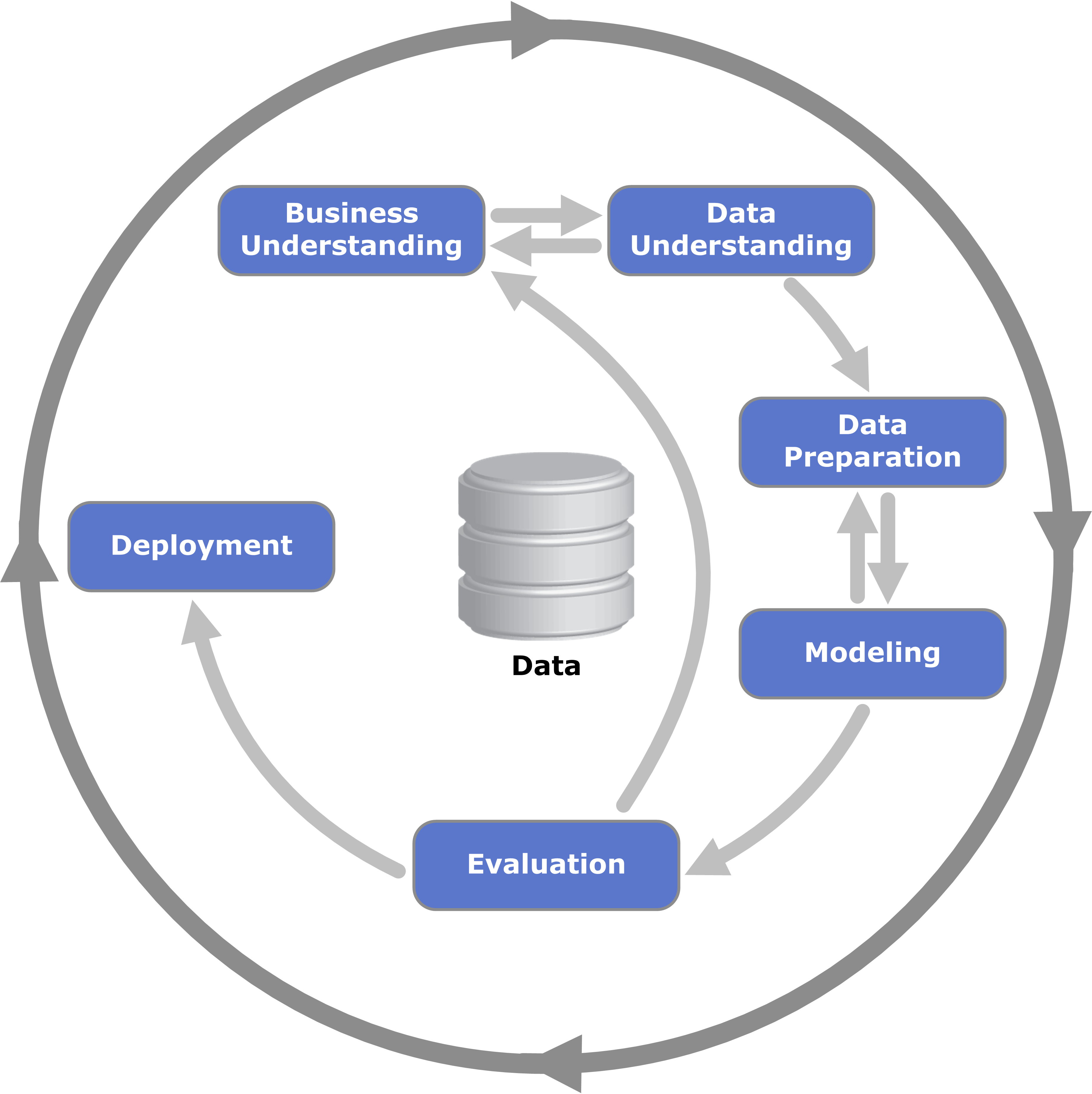
Nous suivons comme d’habitude la méthodologie CRISP-DM
Allez c’est parti !
Nous importons les librairies nécessaires
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline
Compréhension des données
from sklearn.datasets import load_boston
donnees_boston = load_boston()
donnees_boston.keys()
On a le résultat suivant : dict_keys([‘data’, ‘target’, ‘feature_names’, ‘DESCR’])
Le dictionnaire contient data (les informations sur les différentes maisons à boston), target (le prix des maisons), feature_names (noms des différentes caractéristiques du jeu de données) et DESCR (la description du jeu de données).
#On affiche la description du jeu de données
donnees_boston.DESCR.split("\n")
Le résultat est disponible ici Boston Housing data description
Le jeu Contient 506 instances et 13 attributs
-CRIM per capita crime rate by town',
' - ZN proportion of residential land zoned for lots over 25,000 sq.ft.',
' - INDUS proportion of non-retail business acres per town',
' - CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)',
' - NOX nitric oxides concentration (parts per 10 million)',
' - RM average number of rooms per dwelling',
' - AGE proportion of owner-occupied units built prior to 1940',
' - DIS weighted distances to five Boston employment centres',
' - RAD index of accessibility to radial highways',
' - TAX full-value property-tax rate per $10,000',
' - PTRATIO pupil-teacher ratio by town',
' - B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town',
' - LSTAT % lower status of the population',
" - MEDV Median value of owner-occupied homes in $1000's"
MEDV est notre variable à expliquer et les autres sont des variables explicatives.
Préparation des données
On transforme notre jeu de données en un data frame et on vérifie qu’il n’y pas de valeurs nulles.
#Transformation de notre jeu de données en Data Frame grace à pandas
donnees_boston_df = pd.DataFrame(donnees_boston.data, columns=donnees_boston.feature_names)
#on affiche les 5 premières lignes
donnees_boston_df.head()
#on créé une nouvelle colonne qui est PRIX. ce qui equivaut à MEDV du jeu de données
donnees_boston_df['PRIX'] = donnees_boston.target
#on vérifie s'il n'y pas des valeurs nulles
donnees_boston_df.isnull().sum()

On voit qu’il y a aucune valeurs nulles 🙂
Création du modèle
Avant de créer notre modèle on se rend compte qu’on a 13 variables explicatives pour le Prix. Ainsi si on veut être malin on se pose les questions suivantes : dois-je choisir toutes ces variables pour mon modèle ? Quelles sont les variables qui ont une forte relation linéaire avec la variable ‘PRIX’. Pour répondre à ces interrogations on va faire une matrice de corrélation.
Les coefficients de corrélation se situent dans l’intervalle [-1,1].
– si le coefficient est proche de 1 c’est qu’il y a une forte corrélation positive
– si le coefficient est proche de -1 c’est qu’il y a une forte corrélation négative
– si le coefficient est proche de 0 en valeur absolue c’est qu’il y a une faible corrélation.
Comprendre la notion de corrélation
#etude de la correlation
matrice_corr = donnees_boston_df.corr().round(1)
sns.heatmap(data=matrice_corr, annot=True)
On affiche la matrice sous forme de carte thermique (heatmap)

Le prix a une forte corrélation avec LSTAT et RM. Cependant il ne faut pas négliger les autres attributs comme CRIM,ZN,INDUS… car leur corrélation sont pas proches de 0. Il faut savoir que lorsqu’on fait une régression linéaire on pose certaines hypothèses notamment la Non-colinéarité des variables explicatives (une variable explicative ne doit pas pouvoir s’écrire comme combinaison linéaire des autres).
TAX et RAD ont une corrélation de 0.9; NOX et DIS et AGE ont une corrélation de 0.7 ; DIS et INDUS ont une corrélation de 0.7.
Après une analyse minutieuse nous choisissons : LSAT, RM,TAX,PTRATIO
On utilise pour le modèle les variables choisies ci-dessus ensuite on divise notre jeu de données en 2 parties (80%, pour l’apprentissage et les 20% restant pour le test.
#on utilise seulement 4 variables explicatives
X=pd.DataFrame(np.c_[donnees_boston_df['LSTAT'],donnees_boston_df['RM'],donnees_boston_df['TAX'],donnees_boston_df['PTRATIO']], columns = ['LSTAT','RM','TAX','PTRATIO'])
Y = donnees_boston_df['PRIX']
#base d'apprentissage et base de test
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state=5)
print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)
On passe à l’étape suivante : l’entrainement du modèle ! Enfin 😉
#entrainement du modèle
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lmodellineaire = LinearRegression()
lmodellineaire.fit(X_train, Y_train)
Évaluation du modèle de régression linéaire
On utilise deux métriques pour l’évaluation L’erreur quadratique moyenne (l’erreur d’estimation) et le R-square (la qualité du modèle de régression)
le résultat :
# Evaluation du training set
from sklearn.metrics import r2_score
y_train_predict = lmodellineaire.predict(X_train)
rmse = (np.sqrt(mean_squared_error(Y_train, y_train_predict)))
r2 = r2_score(Y_train, y_train_predict)
print('La performance du modèle sur la base dapprentissage')
print('--------------------------------------')
print('Lerreur quadratique moyenne est {}'.format(rmse))
print('le score R2 est {}'.format(r2))
print('\n')
# model evaluation for testing set
y_test_predict = lmodellineaire.predict(X_test)
rmse = (np.sqrt(mean_squared_error(Y_test, y_test_predict)))
r2 = r2_score(Y_test, y_test_predict)
print('La performance du modèle sur la base de test')
print('--------------------------------------')
print('Lerreur quadratique moyenne est {}'.format(rmse))
print('le score R2 est {}'.format(r2))
La performance du modèle sur la base dapprentissage
--------------------------------------
L'erreur quadratique moyenne est 5.303422189850911
le score R2 est 0.6725758894106004
La performance du modèle sur la base de test
--------------------------------------
L'erreur quadratique moyenne est 4.897434387599182
le score R2 est 0.6936559148531631
En somme nous avons dans cet article présenté le concept de la régression linéaire et son implémentation en python. Si vous avez apprécié cet article, je vous conseille vivement de lire notre article sur la régression polynomiale.




Très interessant. Vraiment bien détaillé